速通《hello algo》(一) 了解算法与数据结构
《hello algo》是一本由Krahets大佬主导编写的算法开源书籍,条理清晰、结构合理、深入浅出,非常适合对算法有兴趣的同学用来入门。这个系列的文章将通过对这本书的学习和摘录,来完成自身对算法领域的能力提升以及思维进步。

来源
《hello algo》是一本由Krahets大佬主导编写的算法开源书籍,条理清晰、结构合理、深入浅出,非常适合对算法有兴趣的同学用来入门。这个系列的文章将通过对这本书的学习和摘录,来完成自身对算法领域的能力提升以及思维进步!

引言
算法在日常生活中无处不在,并不是高高在上的凡人不可及的学问。因为算法是要解决现实问题或特定问题的一种步骤,只要我们想要解决问题,就要用到算法。
深入来讲,解决问题的结果大概率就是对数据进行转换、过滤、增减等操作,那么就一定要面对与算法紧紧相随的数据结构——数据结构是算法的基石,用乐高来进行类比的话,那么散落的积木就是数据的输入,而积木组织形式,包括形状、大小、连接方式等就是数据结构,将积木组装成目标形态的过程就是算法,最终的积木就是输出。
算法效率评估
如果通过实际测试来评估算法的效率,成本会非常高,也不现实。所以现在一般采用复杂度分析(Complexity Analysis)和渐进复杂度分析(Asymptotic Complexity Analysis)方法来进行估算。
复杂度分析可以克服实际测试的弊端,分析结果适用于所有运行平台,并且能够揭示算法在不同数据规模下的效率。
时间效率和空间效率是评价算法性能的两个关键维度。也就是时间复杂度和空间复杂度。
两者之间有一套相同的衡量书写方法,用大O表示,即函数渐进上界,也就是说最坏复杂度。最佳复杂度用希腊字母Ω (Omega)来表示,平均复杂度则用Θ (Theta)来表示。一般情况下我们都采用函数渐进上界的方式来表示,因为这是最符合实际场景的。
常见的时间复杂度有常数阶O(1)、对数阶O(log n)、线性阶O(n)、线性对数阶O(n log n)、平方阶O(n²)、指数阶O(2^n)、阶乘阶O(n!)。
常见的空间复杂度有常数阶O(1)、对数阶O(log n)、线性阶O(n)、平方阶O(n²)、指数阶O(2^n)。
数据结构与数据类型
数据结构分类
K神总结的很好,我就不画蛇添足了,摘抄如下:
- 数据结构可以从逻辑结构和物理结构两个角度进行分类。逻辑结构描述了数据元素之间的逻辑关系,而物理结构描述了数据在计算机内存中的存储方式。
- 常见的逻辑结构包括线性、树状和网状等。通常我们根据逻辑结构将数据结构分为线性(数组、链表、栈、队列)和非线性(树、图、堆)两种。哈希表的实现可能同时包含线性和非线性结构。
- 当程序运行时,数据被存储在计算机内存中。每个内存空间都拥有对应的内存地址,程序通过这些内存地址访问数据。
- 物理结构主要分为连续空间存储(数组)和离散空间存储(链表)。所有数据结构都是由数组、链表或两者的组合实现的。
数据类型与编码
计算机中的基本数据类型包括整数byte、short、int、long,浮点数float、double、字符char和布尔boolean。它们的取值范围取决于占用空间大小和表示方式。
数字编码
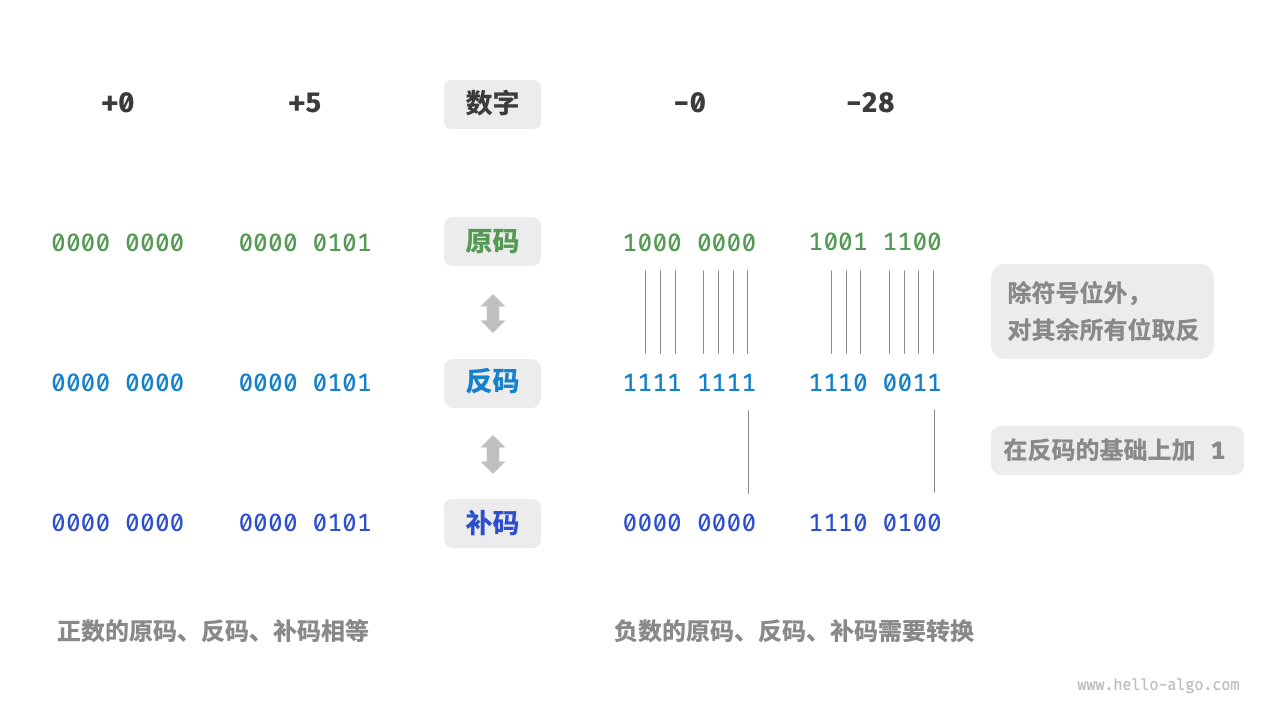
原码、补码和反码时在计算机中编码数字的三种方式,它们之间是可以相互转换的。
- 原码:我们将数字的二进制位表示的最高位视为符号位,其中0表示正式,1表示负数,其余位表示数字的值
- 反码:正数的反码与原码相同,负数的反码是对其原码除符号位以外皆取反
- 补码:正数补码与原码相同, 负数的补码是在其反码的基础上加1
那么为什么要有反码和补码呢?
一方面,负数的原码不能直接用于运算,例如1 + -2 直接运算后的值是-3,这是我们不能接受的。如果通过取反后的反码来进行运算,那1 + -2的结果就是 -1了。
另一方面,计算机中的数字零存在一个+0和-0两种表现方式,这意味着数字零对应着两个不同的二进制编码,而这可能会带来歧义问题。例如,在条件判断中,如果没有区分正零和负零,可能会导致错误的判断结果。如果我们想要处理正零和负零歧义,则需要引入额外的判断操作,其可能会降低计算机的运算效率。与原码一样,反码也存在正负零歧义问题。为此,计算机进一步引入了「补码」。我们可以通过下面的示例来理解补码的意义:
| -0原码 | -0反码 | -0补码 |
|---|---|---|
| 0000 0000 | 1111 1111 | 10000 0000 |
如表所示,在对-0的反码进行补码后,会产生进位,而由于 byte 的长度只有 8 位,因此溢出到第 9 位的 1 会被舍弃。从而得到负零的补码为 0000 0000 ,与正零的补码相同。这意味着在补码表示中只存在一个零,从而解决了正负零歧义问题。
数字编码是一个很有意思的话题,但出于博客的立意,这里就不过多赘述,感兴趣的可以看K神的原文。
字符编码
除了数字编码,还有字符的编码,什么是字符编码,为什么要有字符编码呢?
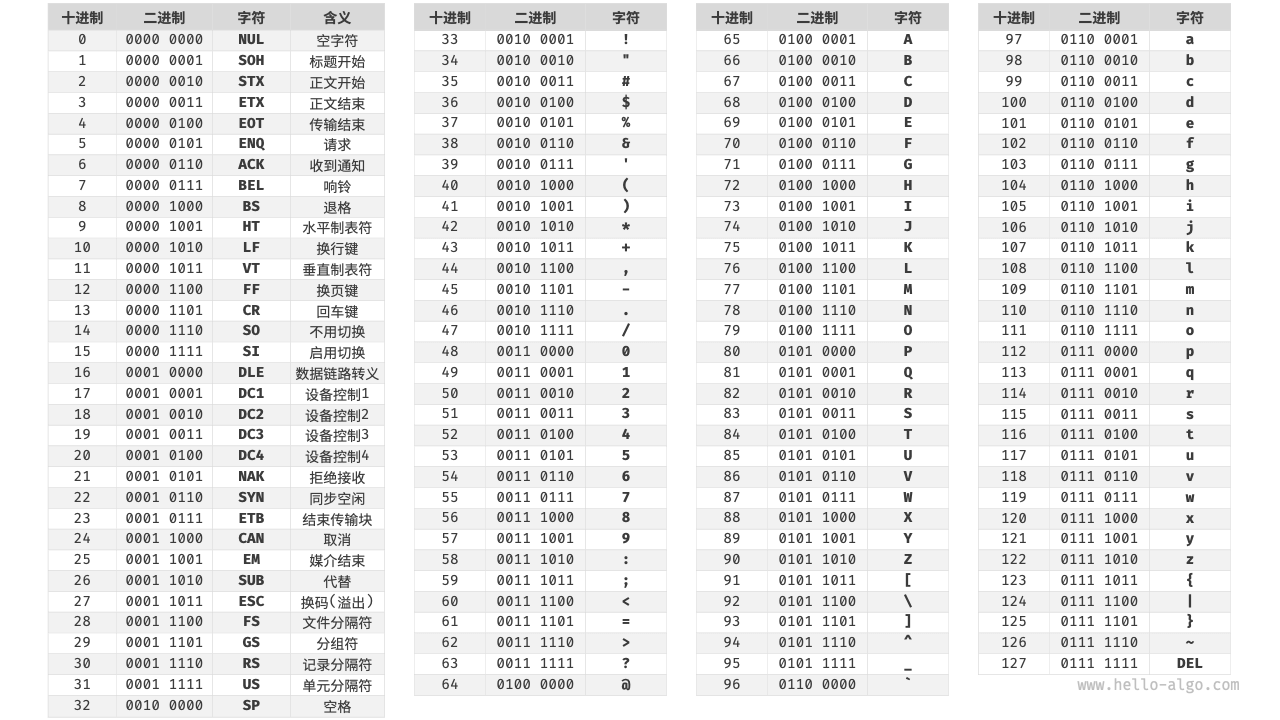
在计算机中,所有数据都是以二进制数的形式存储的,字符 char 也不例外。为了表示字符,我们需要建立一套「字符集」,规定每个字符和二进制数之间的一一对应关系。有了字符集之后,计算机就可以通过查表完成二进制数到字符的转换。时代发展到现在,已经有很多标准字符集诞生并通行了,最早出现的是ASCII字符集,它全称是“美国标准信息交换代码”,它使用 7 位二进制数(即一个字节的低 7 位)表示一个字符,最多能够表示 128 个不同的字符。这包括英文字母的大小写、数字 0-9 、一些标点符号,以及一些控制字符(如换行符和制表符)。
但是ASCII字符集只能表示英文,这不符合计算机全球化的现实需求,所以在ASCII字符集的基础上,诞生了一种能够表示更多语言的字符集「EASCII」。它能够表示 256 个不同的字符。
EASCII虽好,但还是太少,比如对汉字来说它还远远不够。因此,出现了中国国家标准总局于 1980 年发布的「GB2312」字符集,又出现了能处理更多罕见字和繁体字的收录了 21886 个汉字的GBK字符集。(在 GBK 编码方案中,ASCII 字符使用一个字节表示,汉字使用两个字节表示。)
像各国本地化这样的解决办法确实解决了本国的问题,但在全球化交流的历史进程中,多语言环境的交流是一个问题,不同编码标准设备之间的交流也是一个问题。人们就想做一个能涵盖全世界的字符集标准的字符集可以不可以呢?——于是,Unicode应运而生。
截止 2022 年 9 月,Unicode 已经包含 149186 个字符,包括各种语言的字符、符号、甚至是表情符号等。在庞大的 Unicode 字符集中,常用的字符占用 2 字节,有些生僻的字符占 3 字节甚至 4 字节。
到了这里,编码的历史进程还没有结束,因为Unicode虽好,但它在多种长度的 Unicode 码点同时出现在同一个文本中时的解决方案不够完美,太占用空间(它会将不同长度的码点存储成统一长度的编码,英文字符原本只有1字节,但为了和其他语言统一,它就变成了double甚至更多)。所以在Unicode的基础上诞生了最受欢迎的编码方式UTF-8,它是一种可变长的编码,使用 1 到 4 个字节来表示一个字符,根据字符的复杂性而变。
除了 UTF-8 之外,常见的编码方式还包括 UTF-16 和 UTF-32 。它们为 Unicode 字符集提供了不同的编码方法。
UTF-16 编码:使用 2 或 4 个字节来表示一个字符。
UTF-32 编码:每个字符都使用 4 个字节。
对于以往的大多数编程语言,程序运行中的字符串都采用 UTF-16 或 UTF-32 这类等长的编码。这是因为在等长编码下,我们可以将字符串看作数组来处理,具体来说:
- 随机访问: UTF-16 编码的字符串可以很容易地进行随机访问。UTF-8 是一种变长编码,要找到第 i 个字符,我们需要从字符串的开始处遍历到第 i 个字符,这需要 O(n) 的时间。
- 字符计数: 与随机访问类似,计算 UTF-16 字符串的长度也是 O(1) 的操作。但是,计算 UTF-8 编码的字符串的长度需要遍历整个字符串。
- 字符串操作: 在 UTF-16 编码的字符串中,很多字符串操作(如分割、连接、插入、删除等)都更容易进行。在 UTF-8 编码的字符串上进行这些操作通常需要额外的计算,以确保不会产生无效的 UTF-8 编码。
小结
这篇文章主要是对算法和数据结构有个基础的认知,以便接下来细讲数据结构时能知其所以然。本章我们了解了算法复杂度分析的概念和表示方法、数据结构的逻辑结构和物理结构的区别、数字编码的原理以及字符编码的历史进展,相信有了这些理论的铺垫,接下来的阅读和学习会更加顺畅!


